5 star reviews on Amazon

"Provides concrete techniques and tools"

"What's truly fascinating is how accessible these new approaches are"

From the book "You are Solving the Wrong Problem"

Chapter 21: Solutions

Solution to Puzzle 1: Fill in the blank

The letter "e" occurs 8 times already in the sentence. Thus, the words "nine" and "eleven" can be substituted to make the sentence true.

Solution to Puzzle 2: Count to 100 game

This game can be reduced by solving a smaller version of the problem. Consider the same game, except that the game ends with a total of 10 or more. The key is to force your opponent into a losing position by manipulating the total sum on each turn. In this smaller game, you want to move the sum to 9, so that any number after that causes your opponent to reach or exceed 10. You can reach 9 in one move, so you want to go first and say 9.

Now consider the end amount is 20. Using the same principle, you want to land on 19. How can you ensure that happens?

A key observation is that you can manipulate the subtotal of any two moves to add up to 10. We say ten because it is the largest incremental number plus one. Thus, you can cause any two subsequent moves to add up to 10 by saying the number equal to ten minus your opponent's number.

Thus, to guarantee a subtotal of 19 after your turn, you need to make sure you are the one to get to 9. Once the total is nine, you can force it to be 19 after your next turn. Thus, you want to go first in this variation also, so you can say 9.

The key is to understand the properties of small versions of the game. Once you are able to do this, the strategy for the original game emerges. The pattern can be repeated all the way up to 99. Thus, you want to go first in the game and say nine. After that, always say ten minus your opponent's number. This will cause the total to eventually reach 99 and your opponent will lose.

Solution to Puzzle 3: Count to 100, take two

You want to go second. On every move, say the number equal to 11 minus your opponent's number. This will eventually cause the running total to be 99, and your opponent will lose. Note that the strategy is analogous to the first variation of the puzzle, where you say the number equal to 10 minus your opponent's number.

Solution to Puzzle 4: Monty Hall's question

A common intuitive response is that it doesn't matter whether you stick with your initial choice or not. You might think that either unopened door has an equal chance of hiding the car (50-50).

In fact, you should always switch doors if you want to maximize your chances of winning the car. The problem is framed as a continuation of your original choice. However, the second choice (whether to switch doors) is independent. You have new information, and thus, the probability is different.

Thus, the reframed problem is a comparison of two probabilities. You need to compare the probability of your initial choice with the decision to switch. Once you do this, the actual problem becomes clear.

When you initially pick a door, you have a 1/3 chance of choosing the door with the car behind it. Monty then reveals a goat behind one unchosen door. This is always possible, because you choose one door and two doors have goats behind them. Thus, you didn't gain any new information about your initial choice. You did, however, learn more about what is behind the doors.

You now know that, of the three doors, the car must be behind one of the remaining two. If you make a choice now, you have a 2/3 probability. You have already guessed the current door, so the only way to gain these odds is to make the switch. If you stay with your initial choice, your odds remain 1/3. Remember, the reveal didn't change anything about your initial choice.

If you don't believe all of this, you can run a simulation. There are online sites that will help you do this. You will find over the long run, your initial guess will converge to being 33% correct. Making the switch will converge to a 66% accuracy rate. Certainly, 2/3 odds are better than 1/3.

The Monty Hall Problem is a classic illustration of the Problem Paradox. It seems simple at first. Your intuition tells you it shouldn't matter whether you switch because there is still a 50/50. However, the answer is more complex than that. Once we understand it, it then seems simple again.

It's interesting to note that even with faulty probability, you should still switch. The thinking that you have a 50/50 chance represents a better probability than 1/3. Thus, even if you calculated incorrectly, your answer should still be to switch because you don't realize the improved odds until you make the move. Otherwise, you are "stuck" with your original 1/3 odds. This problem demonstrates the importance of asking yourself what is the actual problem. Once you realize that the problem is really a probability comparison, you can determine their independent probabilities and choose the best one.

Solution to Puzzle 5: Burning Island

There is a lot going on in this puzzle. It is helpful to construct a diagram to understand the space and time dimensions.

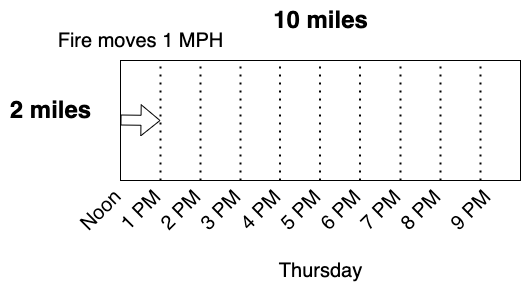
The puzzle description adds a number of constraints regarding the island itself. Specifically, it appears leaving the island is not an option. You are stuck in this rectangular space. The fire will ravage the entire island in 10 hours, and our task is to survive for 12 hours.

After drawing the diagram of the island, it becomes clear that items in the backpack won't help you. This is a space, time, and fire problem. Once we remove the distraction of backpack items and other constraints, the solution space is narrowed. We can focus in on what is important. This eventually leads us to a new problem definition. The actual problem in this puzzle is space creation, not space preservation. Once fire consumes a section of the forest, it is done. Hence, we can create our own space to survive.

You can grab a piece of wood and light it on fire from the west end of the island. If you can't find any wood, perhaps you could use the book as well. Then rapidly take this over to the other side of the island. Stop a good distance away from the East Coast, and start a fire there. The wind will cause this second fire to burn the forest from that point all the way to the East Coast. Once that fire has run its course, you can safely wait in the burnt out area.

This is a classic puzzle that involves space, time, and a basic understanding of the primary element involved, fire. Many details in the puzzle are irrelevant. They serve to increase the potential solution space. They are red herrings, as we noted at the beginning. Even the specific dimensions of the island are largely irrelevant. As long as the fire moves faster than the time and width alloted, you could fill in any numbers.

Solution to Puzzle 6: Clock Face

The majority of people will start using trial and error. They will draw some arbitrary lines, either on paper or in their head, and see what happens. They might get lucky and find the answer. More likely, after a few attempts, they will stop and rethink the approach. Or put the book down and see what’s new on Netflix.

A systematic approach breaks down the problem into a series of smaller steps. What are we actually trying to solve for? If you could decompose the problem into a smaller one, what would it be?

The stated task in the Clock Face puzzle is to draw two lines. The temptation is to focus on the lines first. This is the visual aspect of the puzzle. While this is clearly important, the clock face is really a representation of adjacency on a number line. It’s a visual-not-visual problem (shout out to Arianna Grande).

If you start by trying to draw lines, you are solving the wrong problem. Just like poor swimming technique, you will waste energy and may not reach the finish line. This is a math problem. The answer contains sets of numbers that add up to the same amount. If we work backward, we can figure out what sets of numbers even do this on a clock face.

We can go further backward than that. In order to find those sets, what sums are we looking for? What do valid solutions look like? Well, the sum of all the numbers is 78.

    1+2+...+11+12 = 78

We are only given two lines to draw. Thus, the most regions we can have is four.

    78 ÷ 1 = 78
    78 ÷ 2 = 39
    78 ÷ 3 = 26
    78 ÷ 4 = 17.5

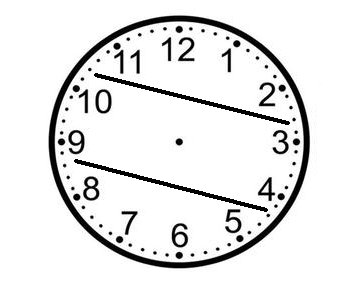
Given two straight lines, there will be at least three sections on the clock face. Based on the math above, there are no solutions with four regions because the numbers don’t add up. Thus, we can focus our search on solutions with 3 sections.

How much of a time-saver is this? It is huge. There are hundreds of permutations that involve two lines. We can rule out the vast majority of them. We can work backward to find subsets of numbers that add up to 26. The complexity of the problem has been reduced. The possible solution space is smaller by an order of magnitude.

The easiest place to start is with the larger numbers, because you reach 26 quickly. Start with 12 and consider a few adjacent numbers. We find that:

    11 + 12 + 1 + 2 = 26

Going down the left side of the clock face, we take 10 and 9 for a subtotal of 19. However, if we add 8, we are over 26.

    10 + 9 + 8 > 26

From our subtotal of 19, we need seven more. The numbers 3 and 4 on the other side of the clock face gives us just that.

    10 + 9 + 4 + 3 = 26

This leaves the region at the bottom which also adds up to 26.

    8 + 7 + 6 + 5 = 26

Note that we did end up using trial and error to solve the puzzle. Once we narrowed the scope of the problem, we tried number combinations until we found the right subsets.

You can find solutions using trial and error when there are only a handful of possibilities. Contrast this to the original problem which had thousands of possibilities. The chance of stumbling upon a solution with these odds is like “finding a needle in a haystack.”

One last thought about this puzzle. Are there other valid solutions? Most puzzles have only one valid solution. Some definitions of the term puzzle literally include this concept. The joy of attempting a puzzle is that we know it does, indeed, have a solution.

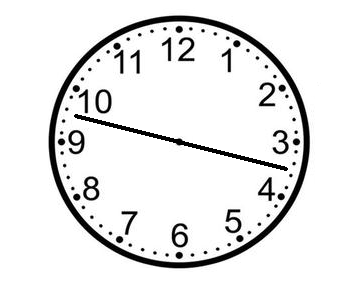
As it turns out, the clock face has a solution made up of only two regions, as shown in Figure 25. However, this would be cheating. The puzzle states that both lines are used to define the regions.

5 star reviews on Amazon

"Provides concrete techniques and tools"

"What's truly fascinating is how accessible these new approaches are"